What is splay tree ? How is it different from a tree ? Explain

 A splay tree is a binary search tree with the additional property that recently accessed elements are quick to access again. Like  self-balancing binary search tree

All normal operations on a binary search tree are combined with one basic operation, called splaying.

Advantages

1. Good performance for a splay tree depends on the fact that it is self-optimizing.

2. Frequently accessed nodes will move nearer to the root where they can be accessed more quickly.

3. Comparable performance: Average-case performance is as efficient as other trees.

4. Small memory footprint: Splay trees do not need to store any bookkeeping data.

Disadvantages

1. The most significant disadvantage of splay trees is that the height of a splay tree can be linear.
2. this will be the case after accessing all n elements in non-decreasing order.
3. Since the height of a tree corresponds to the worst-case access time, this means that the actual cost of a single operation can be high.
4. The representation of splay trees can change even when they are accessed in a ‘read-only’ manner.

Zig step: In this step is done when p is the root.The tree is rotated on the edge between x and p. Zig steps exist to deal with the parity issue, will be done only as the last step in a splay operation, and only when x has odd depth at the beginning of the operation.

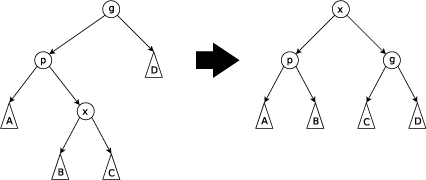
Zig-zig step: this step is done when p is not the root and x and p are either both right children or are both left children. The picture below shows the case where x and p are both left children. The tree is rotated on the edge joining p with its parent g, then rotated on the edge joining x with p. Note that zig-zig steps are the only thing that differentiate splay trees from the rotate to root method introduced by Allen and Munro[4] prior to the introduction of splay trees.

Zig-zag step: this step is done when p is not the root and x is a right child and p is a left child or vice versa. The tree is rotated on the edge between p and x, and then rotated on the resulting edge between x and g.